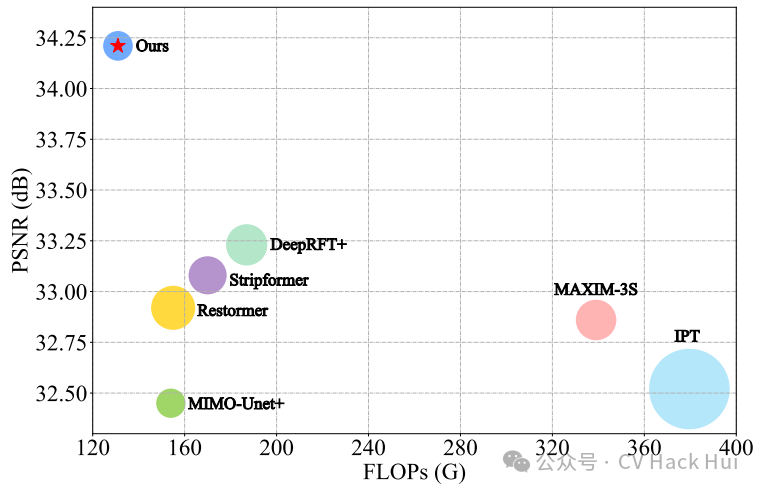
圖像去模糊有突破,新方法適用于所有CV二維任務(wù)?
圖像處理領(lǐng)域里,圖像去模糊技術(shù)一直備受矚目,成為熱門(mén)討論焦點(diǎn)。而傳統(tǒng)方法的不足促使研究者們持續(xù)尋找創(chuàng)新解決方案。
傳統(tǒng)CNN的局限
傳統(tǒng)的卷積神經(jīng)網(wǎng)絡(luò)在圖像去模糊上存在不少缺陷。比如,在處理監(jiān)控?cái)z像頭捕捉的畫(huà)面這類實(shí)際應(yīng)用中,它們主要依賴局部操作。這種做法難以全面把握?qǐng)D像信息。因此,面對(duì)大面積模糊,它們只能局部改善,效果并不理想。而且,從時(shí)間效率來(lái)看,基礎(chǔ)的局部操作速度較慢,因?yàn)樾枰饌€(gè)處理局部區(qū)域,無(wú)法迅速實(shí)現(xiàn)整體去模糊。
面對(duì)傳統(tǒng)方法在處理空間變化特性上的局限,研究路徑亟需調(diào)整。圖像內(nèi)容的空間變化往往復(fù)雜多變,而傳統(tǒng)方法難以有效適應(yīng)這種復(fù)雜性,導(dǎo)致圖像去模糊的效果難以達(dá)到高效和高質(zhì)量。
Transformer的潛力與挑戰(zhàn)
Transformer模型技術(shù)日益進(jìn)步,成為新的期待。在眾多高級(jí)視覺(jué)任務(wù)中,它展現(xiàn)出卓越的全局上下文建模實(shí)力。不論是在科研室的測(cè)試,還是在工業(yè)拍攝場(chǎng)景中的實(shí)際應(yīng)用,其表現(xiàn)都相當(dāng)出色。
Transformer中的scaled dot-product attention機(jī)制存在二次的時(shí)空復(fù)雜度問(wèn)題。這個(gè)問(wèn)題必須引起重視。特別是當(dāng)處理高分辨率圖像時(shí),這種復(fù)雜度會(huì)減慢處理速度,并提升成本。以高端相機(jī)拍攝的高分辨率圖像為例,在去模糊處理過(guò)程中,這種計(jì)算復(fù)雜度的提升會(huì)導(dǎo)致過(guò)程變得異常緩慢,同時(shí)消耗大量資源。
頻域下的解決方案
為了解決這些問(wèn)題,文章提出了一種基于頻域的高效Transformer算法。該方法用元素相乘操作替換了空間域中的矩陣運(yùn)算,以估算縮放點(diǎn)積注意力。這種改動(dòng)非常關(guān)鍵。
從理論層面來(lái)看,元素乘積操作在簡(jiǎn)化復(fù)雜度方面表現(xiàn)更佳。我們無(wú)需執(zhí)行繁復(fù)的矩陣運(yùn)算,仍能實(shí)現(xiàn)相似效果。在具體實(shí)驗(yàn)中,眾多高分辨率圖像在此新法下,處理速度明顯加快。這不僅是理論上的突破,更是實(shí)際應(yīng)用中得以證實(shí)的成效。
高效的頻域自注意力求解器
FSAS求解器應(yīng)運(yùn)而生。該求解器運(yùn)用快速傅里葉變換(FFT)在頻域內(nèi)對(duì)Fq與Fk的相關(guān)性進(jìn)行估算。這一方法依據(jù)卷積定理,即在空間域中進(jìn)行的卷積操作,在頻域中可以轉(zhuǎn)化為逐元素相乘的操作。
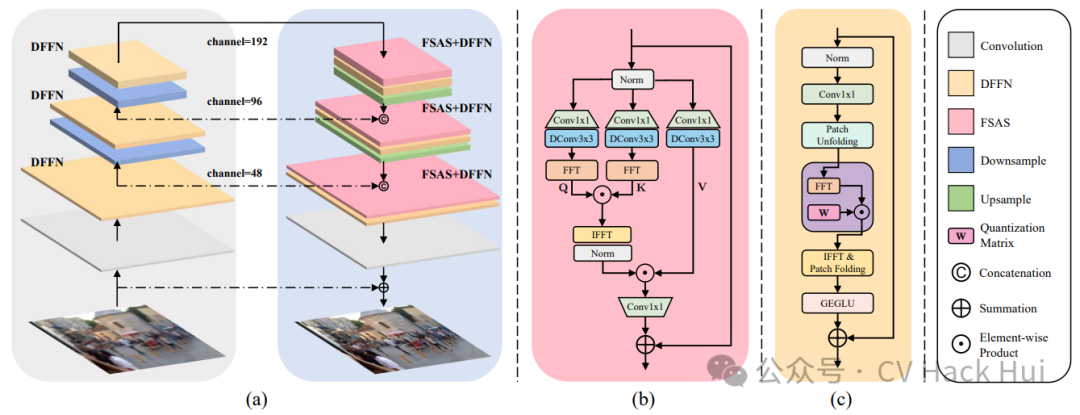
FSAS在很多大型圖像數(shù)據(jù)集中表現(xiàn)突出。它顯著減少了傳統(tǒng)自注意力機(jī)制的計(jì)算負(fù)擔(dān)。從數(shù)據(jù)處理的角度看,它在處理大尺寸、高清晰度圖像時(shí),大幅降低了計(jì)算成本,減輕了噪聲干擾。在眾多圖像編輯軟件的應(yīng)用中,這種改進(jìn)使得用戶在圖像去模糊處理時(shí),能夠獲得更快的速度和更優(yōu)的質(zhì)量。
判別性頻域前饋網(wǎng)絡(luò)

提出了判別性頻域前饋網(wǎng)絡(luò),簡(jiǎn)稱DFFN。此網(wǎng)絡(luò)借鑒了JPEG壓縮技術(shù),并加入了門(mén)控功能。設(shè)計(jì)初衷是為了在恢復(fù)圖像清晰度時(shí),合理選擇保留哪些低頻與高頻信息。

在實(shí)際操作時(shí),不同種類的圖像在低頻與高頻信息上所承載的意義各異。以風(fēng)景照為例,低頻信息通常關(guān)聯(lián)到整體形狀,而高頻則與細(xì)節(jié)緊密相連。通過(guò)這種有目的的信息保留,圖像去模糊的處理效果能更貼合各類圖像的特性,從而更有效地還原圖像的本來(lái)面目。
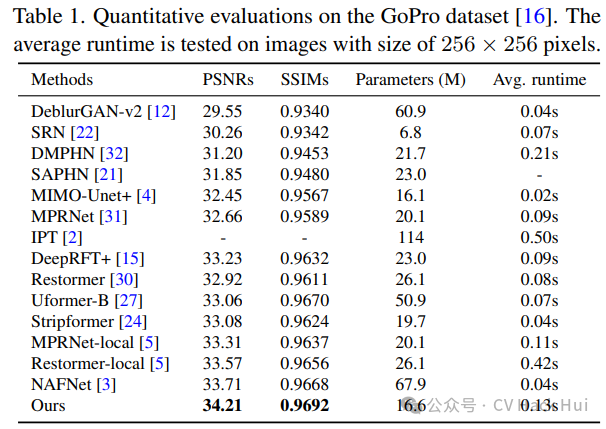
實(shí)驗(yàn)結(jié)果展示
在GoPro數(shù)據(jù)集上進(jìn)行了對(duì)比測(cè)試。結(jié)果顯示,新方法制作出的去模糊圖像,無(wú)論是從PSNR(峰值信噪比)還是SSIM(結(jié)構(gòu)相似性)指標(biāo)來(lái)看,都表現(xiàn)更佳。視覺(jué)效果同樣出色。這表明,結(jié)合了FSAS和DFFN的編碼器-解碼器架構(gòu)網(wǎng)絡(luò)是有效的。該方法具有實(shí)際應(yīng)用價(jià)值,對(duì)圖像去模糊技術(shù)的實(shí)際應(yīng)用具有積極推動(dòng)作用。

最后我想請(qǐng)教各位,關(guān)于圖像去模糊技術(shù),你們認(rèn)為今后還有哪些途徑可以實(shí)現(xiàn)更深入的改進(jìn)?
class FSAS(nn.Module):? ? def?__init__(self, dim, bias=False):? ? ? ??super(FSAS, self).__init__()? ? ? ? self.to_hidden = nn.Conv2d(dim, dim *?6, kernel_size=1, bias=bias)? ? ? ? self.to_hidden_dw = nn.Conv2d(dim *?6, dim *?6, kernel_size=3, stride=1, padding=1, groups=dim *?6, bias=bias)? ? ? ? self.project_out = nn.Conv2d(dim *?2, dim, kernel_size=1, bias=bias)? ? ? ? self.norm =?LayerNorm(dim *?2, LayerNorm_type='WithBias')? ? ? ? self.patch_size =?8? ? def?forward(self, x):? ? ? ? hidden = self.to_hidden(x)? ? ? ? q, k, v = self.to_hidden_dw(hidden).chunk(3, dim=1)? ? ? ? q_patch =?rearrange(q,?'b c (h patch1) (w patch2) -> b c h w patch1 patch2', patch1=self.patch_size,? ? ? ? ? ? ? ? ? ? ? ? ? ? patch2=self.patch_size)? ? ? ? k_patch =?rearrange(k,?'b c (h patch1) (w patch2) -> b c h w patch1 patch2', patch1=self.patch_size,? ? ? ? ? ? ? ? ? ? ? ? ? ? patch2=self.patch_size)? ? ? ? q_fft = torch.fft.rfft2(q_patch.float())? ? ? ? k_fft = torch.fft.rfft2(k_patch.float())? ? ? ? out = q_fft * k_fft? ? ? ? out = torch.fft.irfft2(out, s=(self.patch_size, self.patch_size))? ? ? ? out =?rearrange(out,?'b c h w patch1 patch2 -> b c (h patch1) (w patch2)', patch1=self.patch_size,? ? ? ? ? ? ? ? ? ? ? ? patch2=self.patch_size)? ? ? ? out = self.norm(out)? ? ? ? output = v * out? ? ? ? output = self.project_out(output)? ? ? ? return outputif __name__ ==?'__main__':? ? fsas=?FSAS(32).to(device)? ? input = torch.rand(1,?32,?256,?256).to(device) ?# 輸入張量? ? output =?fsas(input) ?# 前向傳播? ??print(f"n輸入張量形狀: {input.shape}")? ??print(f"輸出張量形狀: {output.shape}")
作者:小藍(lán)
鏈接:http://www.m13746.cn/content/8018.html
本站部分內(nèi)容和圖片來(lái)源網(wǎng)絡(luò),不代表本站觀點(diǎn),如有侵權(quán),可聯(lián)系我方刪除。







